출처 : 위키백과 http://ko.wikipedia.org/wiki/%EB%94%94%ED%94%BC-%ED%97%AC%EB%A7%8C_%ED%82%A4_%EA%B5%90%ED%99%98
디피-헬만 키 교환
디피-헬만 키 교환(Diffie–Hellman key exchange)은 암호 키를 교환하는 하나의 방법으로, 두 사람이 암호화되지 않은 통신망을 통해 공통의 비밀 키를 공유할 수 있도록 한다. 휫필드 디피와 마틴 헬만이 1976년에 발표하였다.
디피-헬만 키 교환은 기초적인 암호학적 통신 방법을 수립하였으며, 이후 1977년 공개 키 암호 방식인 RSA 암호가 제안되었다.
방식[편집]
앨리스와 밥이 공개된 통신망에서 디피-헬만 키 교환을 하기 위해서는 다음과 같은 절차를 거친다.
- 앨리스가 소수
 , 그리고
, 그리고  부터
부터  까지의 정수
까지의 정수  를 선택하여 사전에 밥과 공유한다.
를 선택하여 사전에 밥과 공유한다. - 앨리스가 정수 a를 선택한다. 이 정수는 외부에 공개되지 않으며, 밥 또한 알 수 없다.
- 앨리스가
 , 즉
, 즉 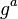 를
를  로 나눈 나머지를 계산한다.
로 나눈 나머지를 계산한다. - 밥이 마찬가지로 정수 b를 선택하여
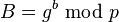 를 계산한다.
를 계산한다. - 앨리스와 밥이 서로에게
 와
와  를 전송한다.
를 전송한다. - 앨리스가
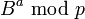 를, 밥이
를, 밥이  를 계산한다.
를 계산한다.
마지막 단계에서  ,
,  이며 따라서 앨리스와 밥은
이며 따라서 앨리스와 밥은 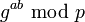 라는 공통의 비밀 키를 공유하게 된다.
라는 공통의 비밀 키를 공유하게 된다.
앨리스와 밥 이외의 인물은 a와 b를 알 수 없으며,  를 알 수 있다.
를 알 수 있다.
예제[편집]
이 과정을 실제 숫자를 통해 예를 들면 다음과 같다. 여기서는 설명을 위해 작은 크기의 소수를 사용하지만, 실제 응용에서는 안전을 위해 10진수 수백~수천자리 크기의 큰 소수를 사용한다. 공개된 정보는 파란색으로, 비밀 정보는 붉은색 굵은 글씨로 표시하였다.
- 앨리스와 밥은 p=23, g=5를 사용하기로 합의한다.
- 앨리스가 비밀 정보를 전송하기 위해 임의의 정수 a=6을 고른 후, 밥에게 A = ga mod p 을 전송한다.
- A = 56 mod 23
- A = 15,625 mod 23
- A = 8
- 밥은 임의의 정수 b=15 를 고르고, 앨리스에게 B = gb mod p 를 전송한다.
- B = 515 mod 23
- B = 30,517,578,125 mod 23
- B = 19
- 앨리스는 밥에게서 받은 B 를 바탕으로 s = B a mod p 를 계산한다.
- s = 196 mod 23
- s = 47,045,881 mod 23
- s = 2
- 밥은 앨리스에게서 받은 A 를 바탕으로 s = A b mod p 를 계산한다.
- s = 815 mod 23
- s = 35,184,372,088,832 mod 23
- s = 2
- 앨리스와 밥은 이제 비밀 키 s = 2 를 공유하게 되었다.
여기서  가 충분히 클 경우, 외부에서 비밀 키를 알아내기 위해 도청을 하는 도청자 이브는
가 충분히 클 경우, 외부에서 비밀 키를 알아내기 위해 도청을 하는 도청자 이브는 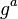 나
나 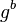 를 통해
를 통해  를 알아낼 수 없는 것으로 알려져 있다. 앨리스와 밥은 두 사람 만이 아는 비밀 키
를 알아낼 수 없는 것으로 알려져 있다. 앨리스와 밥은 두 사람 만이 아는 비밀 키  를 갖게 되었으므로, 대칭 키 암호를 이용해 이후의 통신을 암호화할 수 있다.
를 갖게 되었으므로, 대칭 키 암호를 이용해 이후의 통신을 암호화할 수 있다.
그러나  나
나  ,
,  가 너무 작을 경우, 도청자는 가능한 모든 조합을 다 계산해보는 방식으로
가 너무 작을 경우, 도청자는 가능한 모든 조합을 다 계산해보는 방식으로  를 계산해낼 수 있다. 따라서 실제 비밀 통신에는 충분히 큰 소수를 사용해야 한다. 만약
를 계산해낼 수 있다. 따라서 실제 비밀 통신에는 충분히 큰 소수를 사용해야 한다. 만약  가 최소 300자리의 소수이고,
가 최소 300자리의 소수이고,  와
와  가 각각 100자리 이상의 정수일 경우, 현재 인류가 보유한 모든 컴퓨터를 동원해도 공개된 정보로부터 비밀 키를 알아낼 수 없는 것으로 알려져 있다.
가 각각 100자리 이상의 정수일 경우, 현재 인류가 보유한 모든 컴퓨터를 동원해도 공개된 정보로부터 비밀 키를 알아낼 수 없는 것으로 알려져 있다.
안전성[편집]
디피-헬만 키 교환은 소수  와
와  를 적절하게 고르면 도청에 대해 안전한 것으로 알려져 있다. 도청자 이브가 비밀키를 얻어내기 위해서는 앨리스와 밥 사이의 통신에서 도청할 수 있는 정보인
를 적절하게 고르면 도청에 대해 안전한 것으로 알려져 있다. 도청자 이브가 비밀키를 얻어내기 위해서는 앨리스와 밥 사이의 통신에서 도청할 수 있는 정보인 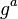 와
와 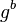 로부터
로부터 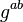 를 구해야 한다. 이 문제를 디피-헬만 문제(Diffie-Hellman problem)로 부르며, 이 문제를 푸는 효율적인 알고리즘은 2013년 현재 알려지지 않았다. 이산 로그 문제를 효율적으로 풀 수 있을 경우 디피-헬만 문제 또한 효율적으로 풀 수 있지만, 그 역이 참인지는 알려지지 않았다.
를 구해야 한다. 이 문제를 디피-헬만 문제(Diffie-Hellman problem)로 부르며, 이 문제를 푸는 효율적인 알고리즘은 2013년 현재 알려지지 않았다. 이산 로그 문제를 효율적으로 풀 수 있을 경우 디피-헬만 문제 또한 효율적으로 풀 수 있지만, 그 역이 참인지는 알려지지 않았다.
안전한 키 교환을 위해서는  와
와  를 신중하게 선택해야 한다.
를 신중하게 선택해야 한다.  는 순환군
는 순환군  의 차수가 소수이거나, 인수분해하기 어려운 큰 소수를 약수로 갖도록 해야 한다. 이 때문에
의 차수가 소수이거나, 인수분해하기 어려운 큰 소수를 약수로 갖도록 해야 한다. 이 때문에  와
와 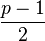 이 모두 소수인 안전 소수를 고르기도 한다.
이 모두 소수인 안전 소수를 고르기도 한다.  가 안전 소수일 경우
가 안전 소수일 경우  의 차수는
의 차수는  또는
또는 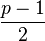 만을 약수로 갖게 된다.
만을 약수로 갖게 된다.
또한 앨리스와 밥이 충분히 안전하지 못한 난수 생성 알고리즘을 사용할 경우, 공격자는 이를 이용해 다음  와
와  의 특성을 어느정도 예측할 수 있다.
의 특성을 어느정도 예측할 수 있다.
디피-헬만 키 교환은 통신을 하는 대상과 비밀 정보를 공유할 수 있지만, 상대방에 대한 인증은 보장되지 않으며 중간자 공격이 가능하다. 앨리스와 밥이 상대방에 대한 인증을 하지 못할 경우, 공격자는 중간에서 통신을 가로채 앨리스와 공격자, 그리고 공격자와 밥 사이에 각각 두 개의 디피 헬만 키 교환을 생성하고, 앨리스와 밥이 각각 서로와 통신을 하는 것처럼 위장할 수 있다. 이와 같은 종류의 중간자 공격을 막기 위한 여러가지 다른 알고리즘이 개발되어 있다.
'Dev > Encryption' 카테고리의 다른 글
| SHA1 해쉬함수, boost 라이브러리로 구현 (0) | 2014.10.22 |
|---|---|
| 디피-헬만 키 교환, C++ 예제 (0) | 2014.10.17 |
| SSL 키 교환 방식 (0) | 2014.10.15 |
| 해쉬 함수 SHA1CryptoServiceProvider, SHA1Managed 차이 (0) | 2014.09.26 |
| Crypto++ 사용하기, 예제 (2) | 2009.10.14 |